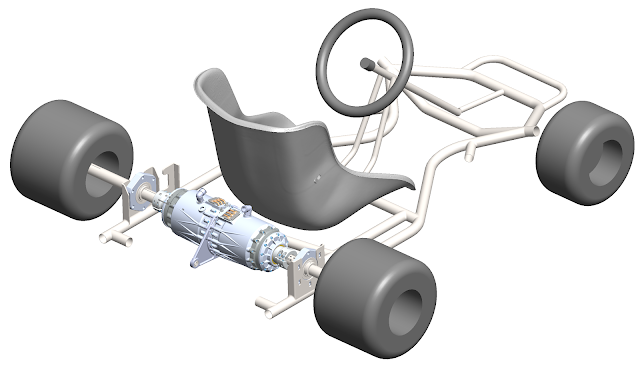
As I've mentioned in previous posts, robot land has an annual car-and-other-vehicle show. Last year I brought the trike, but the year before that I brought the electric kart I worked on with Bayley.
 |
| Picture from Bayley |
Before the event, the kart hadn't been touched since the pre-Covid days. Bringing it back to life and ripping around the parking lot was a great reminder of two things:
- This thing is so much fun to drive.
- Thing is so janky
A few parts of the kart were mechanically nice like the polychain pulley system, but the rest of the kart mechicals were bodged together out of literal garbage from the miters floor (not my fault, honest). Not even joking, the tube holding up the inverter is a piece of electrical conduit.
Anyways, this got me motivated to make the cart not awful - which basically means re-doing just about everything. The drivetrain isn't the most offensive part of the kart, but I'm starting there, since it involves motors and gears.
Step 1, actually make a CAD model of the kart. I sketched out the chassis dimensions and solidworks'd up a model. I brought the fiberglass Tillett seat into work and got a 3D scan of it with Bill's help.
One feature I wanted with this upgrade was independent control of the rear wheels rather than a solid rear axle - so I can do fun traction control stuff in the future. There are some complications making this work well on a kart chassis (which are designed around solid axles and jacking up the inner wheel around corners), but I have plans to deal with that I'll explain in some other post. I explored a few different layouts for independent drive units - sticking with belts and single-stage spur or helical gear reductions were the two main other candidates - but a pair of planetary drive units in-line with the rear axle looked the most promising.
For motors, I'm using the hybrid starter generators (HSG's) from the 2017 Ioniq hybrid. The kart originally used a pair of 2012 Sonata Hybrid HSG's. 2 years ago I got one of the Ioniq HSG's to tear down and take some measurements on (this project has been brewing for a while), and found that the terminal measurements (resistance, inductances, back-emf) were identical to the older Sonata HSG's, but the motor was slightly smaller and a couple kg's lighter.
 |
| V-magnet arrangement rather than flat magnets like the 2012 HSG |
Carefully freeing the stator from its housing with a hacksaw:
I looked into a few different options for planetary gears and ended up buying some chinese industrial servo planetaries in the hopes I could modify them to work. Assuming this would work it was dramatically cheaper than using off-the-shelf or custom made gears. They look absolutely enormous as they came, but I was pretty sure these had a lot more steel than they really needed.
I took apart the gearboxes, modeled them, and figured out where I could hack away material. I was able to substantially reduce the length of the gearbox, and shave 5.6 kilograms off its weight as-received, getting it down to 2.6kg. Not as quite as light as the old belt system, but the overall assembly should end up a fair bit lighter than the old motors + pulleys + mounting brackets. A lot of the mass and size savings was from going down a cross section size on the output bearings - the stock bearings were much beefier than I needed.
For re-housing the motors, I tried out PCBWay's aluminum 3d printing services. Printing the housing let me integrate a waterjacket into a monolithic housing, and was cheaper than getting the housings machined from multiple parts out of billet.
For the waterjacket I did a counterflow design, mostly for mechanical reasons so the inlet and outlet would be right next to each other. I added ribs down the water channels to add surface area and reduce the pressure drop around the 180 bend (top left in the picture below). Not that I actually did any heat exchanger math or CFD to back up this design. If the stock waterjacket was adequate this should be good enough....
The yellow surfaces on the model below were post-machined. These all had 1.5mm-2mm extra material added for machining away
Cross section of the full drive unit:
In context on the kart:
The PCBWay printed housings turned out great - they must have done a ton of hand finishing work, there were no traces of support material left on the build platform side of the part. They were designed to be printed motor bore up, so all the circular features were in the print plane and ended up very concentric and close to nominal size.
One distortion showed up in the prints - there was some shrinkage in the outer diameter of the part where the ribs in the water channel are. Not surprising given the thin outer wall (1.5mm) and the sudden change in cross section at the ribs.
I didn't order any spare housings (they were cheap for a metal 3d print this big but not that cheap), so I had no opportunity to screw up the post machining.
Post machining step 1 was the front side of the motor housing - the gearbox interfaces and front bearing bore. To hold the housings I made an expanding mandrel to grip the un-machined motor bore. The expanding mandrel is basically a collet with a cylindrical OD and tapered ID. The collet is pushed axially down a tapered shaft to expand and grip the ID of the part.
Mandrel 3d-printed on the Bambu printer. Printed in PETG with solid 5mm thick walls.
 |
| The tapered shaft part of the fixture |
To get the fixture to run true I skimmed the outside in-place on the lathe. A single M8 bolt and a big aluminum washer clamp the mandrel axially to expand it.
Housing mounted - this is actually after machining, somehow didn't get any pictures before finishing the turning.
Runout on the un-machined surfaces turned out surprisingly good for fixturing and measuring off printed surfaces.
First operation finished on both parts:
To machine the stator side of the housing, I made a fixture that located the parts on one of the features turned in the last op. Held in the 4-jaw chuck so I could indicate the fixture back in true if needed:
Runout on the as-printed motor bore after fixturing. After post-machining there would be some nominally 1 and 1.5mm thick walls, so I didn't have a ton of wiggle room:
Large thin-walled parts like this are prone to ringing during machining. To damp out vibrations better I wrapped the housings in a bicycle inner tube - see video below of before/after ringing.
All the turning finished:
Some video from the turning process:
The milling was pretty simple - nothing tight tolerance, just a bunch of tapped holes and a few faces milled flat. I set up the housings on the Bridgeport using the same fixture as the previous turning step:
Indicating it in for the hole patterns on the other side:
For the side operations I held the housing in the vise with some over-sized vise jaws. The side features were aligned to the previously drilled holes, so I could use the holes for alignment rather than having to indicate the part in level:
Finally, tapping the threads for water cooling fittings. There wasn't much clearance in the water channel, so I had to grind off the tip of the tap in order to tap to full depth. In retrospect I should have made the bosses for the fittings a millimeter or two taller.
I preemptively helicoiled all the structural M4 threads on the part - the printed aluminum alloy (AlSi10Mg) is similar strength to 6061, so not particularly strong.
I got even more use out of the stator fixture for installing the stators. I added a guide rod to the fixture, concentric to the motor housing:
I 3d-printed a flexure to guide the stator into the housing - the flexure is a light press into the ID of the stator, and designed to be stiff in tilting but compliant in X/Y. This keeps the stator axis parallel to the housing axis, but lets the stator center itself on the housing bore:
The stator was a light interference fit into the housing and secured with retaining compound. I heated up the housing to around 100C with a wrap-around heater to open up the housing and slip the stator into place. I did the assembly in a pneumatic-driven hydraulic press, I could send the stator home with the press if it got stuck half way down:
Most of the work modifying the gearboxes was machining the housing/ring gear. The bulk material removal was done on the lathe at work - I tried at home but my little Clausing wasn't stiff enough to handle interrupted cuts in tough steel on a 6" diameter part.
After turning there was some profiling, hole-drilling, and counterboring on the tiny 5-axis mill. It made terrible noises but did the job:
Both ring gears after some hand-tapping and deburring
I made a new rotor shaft for the Ioniq motor to interface directly with the sun gear. These were turned out of 4140 HT bar (pre-heat-treated to ~32 HRC) on the Clausing:
 |
| I roughed with inserts for steel, but the polished insert for aluminum left a fantastic finish on light finishing passes |
 |
| Nice |
The front is threaded for a lockring that clamps the front rotor bearing:
Bearing and lockring test fit:
Here's the new shaft next to the original. The original used a straight knurle press fit to transfer torque from the rotor lamination stack. I went with a straight press-fit with retaining compound since it's simpler and not a super high stress interface.
The sun gear is held in with a heavy press fit + retaining compound. I copied the amount of interference from the original gearbox shaft:
I put a generic M6 tap + 15mm bore interface on the back of the rotor for encoders. Eventually I'll probably switch to a magnetic encoder, but right now I've attached the stock resolvers since that's what the kart's electronics are set up to deal with
 |
| I may get the rotors re-balanced, apparently it's not to expensive and the balance has probably changed with the new shafts. |
Rotor installed in the drive unit:
The output of the gearbox clamps directly on the keyed go-kart axle. I shortened the stock output shaft on the planet carrier, tapped a hole pattern in it, and machined some clamping shaft couplings that bolt to the face of the carrier. This part does double-duty clamping the inner race of the bearing on the front of the gearbox
 |
| Planet carrier milling. Planets taped up so swarf doesn't get in sensitive places |
I broke out my old lathe-broaching tools and single-point broached the 6mm keyway on the lathe:
Gear box re-assembly with new bearings. I splurged a bit on legit NSK brand bearings:
Gearbox assembled with the new front plate (sent out to have this machined and anodized black) and output coupling:
And there it is, an assembled drive unit:
Giving it a spin with one of my little motor drives:
I was hoping to get the kart driving again this summer, but ended up doing (and preparing for) other things.