An idea I've had in the back of my head for a while now is using varying transmission ratios to transfer kinetic energy between bodies. That sounds really abstract, but I'll explain.
Here's a simple example that frames the problem.
There's a mass, \(m\), which can translate in \(x\). Driving the mass is an actuator with inertia \(j\) and angle \(\theta\). There's a transmission between the rotation of the actuator and the translation of the mass. The transmission ratio, \(k\), is the ratio between angular velocity of the actuator and linear velocity of the mass, i.e. a radius. This radius varies as the angle of the actuator changes.
Below is a sketch of how a varying transmission ratio might look, with a pulley that changes radius as it winds up:
The specific idea I wanted to test out was this:
Start out with a low transmission ratio, so spinning the inertia doesn't move the mass very much. "Spool up" the inertia to high speed. Vary the transmission ratio so the mass accelerates at constant power, but the inertia speed is constant. Then, rapidly increase the transmission ratio. This should cause the inertia to decelerate, transferring its kinetic energy to the mass.
At least, that's intuitively what I would expect to happen. It's similar to the idea of revving up an engine and dumping the clutch to accelerate hard (or do a burnout), but in the clutch case, half of the kinetic energy is necessarily dissipated by slip in the clutch. In the variable transmission ratio case, there's no slip, so there shouldn't be any energy loss.
Jumping into the dynamics:
Instantaneously, the relationship between angular velocity and linear velocity is:
There's a mass, \(m\), which can translate in \(x\). Driving the mass is an actuator with inertia \(j\) and angle \(\theta\). There's a transmission between the rotation of the actuator and the translation of the mass. The transmission ratio, \(k\), is the ratio between angular velocity of the actuator and linear velocity of the mass, i.e. a radius. This radius varies as the angle of the actuator changes.
Below is a sketch of how a varying transmission ratio might look, with a pulley that changes radius as it winds up:
The specific idea I wanted to test out was this:
Start out with a low transmission ratio, so spinning the inertia doesn't move the mass very much. "Spool up" the inertia to high speed. Vary the transmission ratio so the mass accelerates at constant power, but the inertia speed is constant. Then, rapidly increase the transmission ratio. This should cause the inertia to decelerate, transferring its kinetic energy to the mass.
At least, that's intuitively what I would expect to happen. It's similar to the idea of revving up an engine and dumping the clutch to accelerate hard (or do a burnout), but in the clutch case, half of the kinetic energy is necessarily dissipated by slip in the clutch. In the variable transmission ratio case, there's no slip, so there shouldn't be any energy loss.
Jumping into the dynamics:
Instantaneously, the relationship between angular velocity and linear velocity is:
$$\dot{x} = k\dot{\theta}$$
Differentiating, the relationship between accelerations is:
$$\ddot{x} = k\ddot{\theta} + \dot{k}\dot{\theta}$$
Normally, with a fixed transmission ratio, \(\ddot{x} = k\ddot{\theta}\). But if the transmission ratio isn't constant, another term shows up. If the transmission ratio is increasing and there's positive angular velocity, there's an additional positive acceleration. That's in-line with the intuition so far.
If a constant torque \(\tau\) is applied to the actuator, the acceleration of the mass works out to the following:
$$
\ddot{x} = \frac{k\tau + j\dot{k}\dot{\theta}}{j + k^{2}m}
$$
Rather than the transmission ratio being time-varying, say it's position-varying. Imagine a cable spooling up on a variable-radius pulley, or a cam follower rolling along a cam. Recognizing that if \(k = k(\theta)\), then \(\dot{k} = \dot{\theta}\frac{dk}{d\theta}\), the acceleration is:
$$
\ddot{x} = \frac{k\tau + j\dot{\theta}^{2}\frac{dk}{d\theta}}{j + k^{2}m}
$$
This position-derivative variant is nice because it can be pre-computed from k vs position, rather than requiring time-differentiation to get.
Going back to the idea I wanted to test: Spool up the motor to high speed. Operate at constant speed and power. Then spool down the motor to transfer the actuator's kinetic energy to the mass.
I roughly hand-designed a varying transmission ratio to do this. At the beginning, there's a constant, small transmission ratio. Then it switches to a logarithmic curve - A log curve results in constant power output at constant actuator angular velocity, although I'm not going to justify that here. At the end, it rapidly increases to slow down the actuator.
Here's a plot of the example transmission ratio vs motor angle. Polar version of the plot on the right:

And a rotating GIF for good measure:
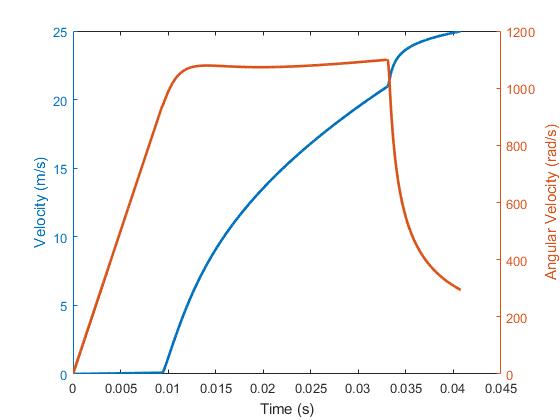
Simulating the dynamics, here's what I get when applying a constant torque to the actuator. Actuator angular velocity and speed of the mass are plotted below. First, when the transmission ratio is tiny, the angular velocity ramps up but the mass barely moves. Then when the transmission reaches the logarithmic section, the angular velocity becomes roughly constant. The mass accelerates at constant power. Finally, the steep end section of the transmission is reached, the actuator angular velocity quickly decreases, and there is a corresponding jump in mass linear velocity.
Plotting the kinetic energies of the actuator and mass, vs the input energy, \(\int{\tau\omega}\), you can clearly see energy trading off between the actuator and mass. No energy is lost - the kinetic energies at the end are equal to the input energy:
Changing gears (ha), here's what a solid model of a pulley with this profile looks like:
And rather than a variable-radius pulley, the same transmission profile can also be implemented as a variable-pitch screw (or maybe technically a barrel cam). A pair of cam followers ride in the grooves and act as the nut:
Stay tuned, prototypes coming up soon.
If a constant torque \(\tau\) is applied to the actuator, the acceleration of the mass works out to the following:
$$
\ddot{x} = \frac{k\tau + j\dot{k}\dot{\theta}}{j + k^{2}m}
$$
Rather than the transmission ratio being time-varying, say it's position-varying. Imagine a cable spooling up on a variable-radius pulley, or a cam follower rolling along a cam. Recognizing that if \(k = k(\theta)\), then \(\dot{k} = \dot{\theta}\frac{dk}{d\theta}\), the acceleration is:
$$
\ddot{x} = \frac{k\tau + j\dot{\theta}^{2}\frac{dk}{d\theta}}{j + k^{2}m}
$$
This position-derivative variant is nice because it can be pre-computed from k vs position, rather than requiring time-differentiation to get.
Going back to the idea I wanted to test: Spool up the motor to high speed. Operate at constant speed and power. Then spool down the motor to transfer the actuator's kinetic energy to the mass.
I roughly hand-designed a varying transmission ratio to do this. At the beginning, there's a constant, small transmission ratio. Then it switches to a logarithmic curve - A log curve results in constant power output at constant actuator angular velocity, although I'm not going to justify that here. At the end, it rapidly increases to slow down the actuator.
Here's a plot of the example transmission ratio vs motor angle. Polar version of the plot on the right:

And a rotating GIF for good measure:
Simulating the dynamics, here's what I get when applying a constant torque to the actuator. Actuator angular velocity and speed of the mass are plotted below. First, when the transmission ratio is tiny, the angular velocity ramps up but the mass barely moves. Then when the transmission reaches the logarithmic section, the angular velocity becomes roughly constant. The mass accelerates at constant power. Finally, the steep end section of the transmission is reached, the actuator angular velocity quickly decreases, and there is a corresponding jump in mass linear velocity.
Plotting the kinetic energies of the actuator and mass, vs the input energy, \(\int{\tau\omega}\), you can clearly see energy trading off between the actuator and mass. No energy is lost - the kinetic energies at the end are equal to the input energy:
Changing gears (ha), here's what a solid model of a pulley with this profile looks like:
And rather than a variable-radius pulley, the same transmission profile can also be implemented as a variable-pitch screw (or maybe technically a barrel cam). A pair of cam followers ride in the grooves and act as the nut: