Getting back to this mechanism. In the post about the dynamics with varying transmission ratio, I came up with the design for the transmission profile by a combination of hand-calculations, intuition, and guesswork. But we can do better.
This problem fits nicely into a trajectory optimization. For an intro to trajectory optimization, I'd highly recommend this MIT Underactuated Robotics chapter.
I not-so-subtly hinted that the point of this mechanism was for jumping or launching things with an electric motor. The simple English explanation of what I'm trying to do with a trajectory optimization here is answer this question: What transmission ratio vs time maximizes jump height without breaking the mechanism?
The optimization-lingo version of that would be something like:
Minimize \(-\dot{x}(t_{final})\), subject to:
- Dynamics are not violated (i.e. \(x(t) = \int_{t_{0}}^{t_{final}} \dot{x}\,dt + x(t_{0})\))
- Initial conditions (everything starts at rest, i.e. \(x(t_{0})=0\), \(\dot{x}(t_{0})=0\), etc)
- \(\ddot{x} < a_{max}\), \(\omega < \omega_{max}\) (acceleration limit to limit forces, maximum motor speed)
- And a few other things I'll get to later
I set up the problem using CasAdi, which is the same tool Jared and I used for the Mini Cheetah backflip optimization. CasAdi makes it super easy to set up nonlinear optimizations like without having to understand what's going on in the back-end too deeply.
Walking through my code (on GitHub here):
Pick some constants
The only "choice" here is the number of trajectory intervals. Roughly speaking, too few will result in integration error, and too many will take longer to converge. Everything else is just physical parameters:
1
2
3
4
5
6
7
8 |
N = 200 # number of trajectory intervals
m = .75 # mass (kg)
j_rotor = 6e-6 # rotor inertia (kg*m^2)
l_leg = .35 # leg length (m)
tau = 1.6 # motor torque (N-m)
w_max = 1200 # max motor speed (rad/s)
g = 9.8 # gravity (m/s^2)
|
Decision variables
I took a "Direct Transcription" approach to the optimization - at each point along the trajectory, both the state (positions, velocities) and control inputs (transmission ratio and its derivative) are decision variables being optimized for. As someone with not very much experience with this stuff, I found this easier to understand and implement than other methods (see here for several formulations). I end up with a ton of redundant decision variables here (really there's only one independent one, which is the transmission ratio), but having position and velocity and acceleration and motor angular velocity and transmission ratio derivative as decision variables makes it very easy to put constraints on those terms.
Another note here, I have the final takeoff time as a decision variable. This seems to usually not be a good idea (I won't pretend I can do an explanation justice), but this problem is simple enough that it works out. Doing the Mini Cheetah backflips, for example, we did not do this, and fixed the takeoff times ahead of time (and did a little manual tuning to get the optimization to produce a nice result). But that optimization had way more states and control inputs than this one.
Also, CasAdi is great. foo = opti.variable(rows, cols), and you have a matrix of decision variables.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | opti = Opti() # Optimization problem
### decision variables ###
X = opti.variable(2,N+1) # position and velocity trajectory
pos = X[0,:]
speed = X[1,:]
accel = opti.variable(1, N+1) # separating this out behaved better than including in X
U = opti.variable(2,N+1) # transmission ratio and its derivative
k = U[0,:]
kd = U[1,:]
W = opti.variable(2, N+1) # rotor angle and angular velocity
theta = W[0,:]
thetad = W[1,:]
T = opti.variable() # final time
|
Pick a cost function
Often it's hard to describe what you "want" the optimization to do in an equation, have multiple competing objectives, and so on, but this problem is charmingly simple. Maximizing jump height is the same as maximizing takeoff velocity, so we just minimize the negative of that.
1
2 | #### objective ###
opti.minimize(-(speed[-1])) # maximize speed at takeoff
|
Set up the dynamics constraints
This is the real meat of the optimization. It implements the varying transmission ratio dynamics (with gravity this time) at every timestep along the trajectory.
The equations of motion,
$$
\ddot{x} = \frac{k\tau + j\dot{k}\dot{\theta}-k^{2}mg}{j + k^{2}m}
$$
are implemented by the function \(f(x, u)\). \(x\) is really the vector \([x, \dot{x}]\) at the timestep being evaluated, and u, the control input, is the transmission ratio and its derivative, \([k, \dot{k}]\). It returns \([\dot{x}, \ddot{x}]\).
To ensure the dynamics are respected, there's trapezoidal integration constraints at each timestep, for all the states. Basically, \(x(t+\Delta t) = x(t) + \Delta t\frac{(\dot{x}(t) + \dot{x}(t+\Delta t)}{2}\), and same deal for \(\dot{x}\), \(k\), \(\dot{k}\), and \(\omega\).
Finally there's the transmission ratio constraint, \(\dot{x} = k\dot{\theta}\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | #### dynamic constraints ###
f = lambda x,u: vertcat(x[1], (u[0]*tau + j_rotor*x[1]*u[1]/u[0] - m*g*(u[0]**2))/(j_rotor + m_body*(u[0]**2))) # dx/dt = f(x,u)
dt = T/N # length of a control intervals
for i in range(N): # loop over control intervals
k1 = f(X[:,i], U[:,i])
k2 = f(X[:,i+1], U[:,i+1])
x_next = X[:,i] + dt*(k1+k2)/2 # trapezoidal integration
opti.subject_to(X[:,i+1]==x_next) # dynamics integration constraint
opti.subject_to(accel[i] == k1[1]) # acceleration
k_next = k[i] + dt*(kd[i] + kd[i+1])/2 # transmission ratio integration constraint
opti.subject_to(k[i+1]==k_next)
theta_next = theta[i] + dt*(thetad[i] + thetad[i+1])/2
opti.subject_to(theta[i+1] == theta_next) # angle/angular velocity integration constraint
opti.subject_to(thetad[i] == speed[i]/k[i]) # linear and angular velocity transmission ratio constraint
|
Bounds and boundary conditions:
The bounds are hard limits on the range of values the decision variables are allowed to take. These are mostly based on physical constraints of building a variable transmission. There are bounds on the derivative of the transmission ratio, so it doesn't instantaneously jump. There are bounds on the transmission ratio itself, because it can't be infinite or too small. The motor has a maximum angular velocity. There's an acceleration limit to limit the forces on the transmission.
In addition to the bounds, there are some constraints on the initial and final state. Everything has to start at rest at 0 position and velocity. At the end, the extension of the "leg" should be the length of the leg. The final motor speed should be small, so it doesn't crash into a hard-stop with too much energy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | ### bounds ###
opti.subject_to(opti.bounded(0,kd,50)) # transmission ratio derivative bounds (no infinite slopes)
opti.subject_to(opti.bounded(0.0008,k,1)) # transmission ratio bounds (meters per radian)
opti.subject_to(opti.bounded(0, thetad, w_max)) # maximum motor angular velocity
opti.subject_to(opti.bounded(.01, T, .5)) # reasonable takeoff time limits
opti.subject_to(opti.bounded(0, accel, 1000)) # acceleration limits
#### boundary conditions ###
opti.subject_to(pos[0]==0) # 0 initial position
opti.subject_to(speed[0]==0) # 0 initial velocity
opti.subject_to(pos[-1]==l_leg) # final position = leg length at takeoff
opti.subject_to(theta[0] == 0) # initial rotor angle of zero
opti.subject_to(thetad[-1]<200) # final rotor speed < 200 rad/s
opti.subject_to(thetad[-1] == speed[-1]/k[-1]) # linear and angular velocity transmission ratio constraint at the end
#### misc. constraints ###
opti.subject_to(T>=0) # Time must be positive
|
Initial guess
The initial guess is the values for the decision variables that the optimization algorithm starts from. For weird nonlinear trajectory optimizations, good initial guesses can make an enormous difference in the convergence speed and quality of the solutions. A good example from my old lab is Gerardo's regularized predictive controller, which, as a flavor non-linear model predictive controller (MPC), runs a trajectory optimization at ~100 hz, so it can be used for (incredibly impressive) feedback control. One of the many things that lets that optimization run at 100 hz is a good initial guess (a.k.a. "warm starting").
But this problem's simple, so I did a few runs starting from guesses of zero for everything, and picked what looked like the "average" values of the solutions I got as the new initial guesses.
1
2
3
4 | #### initial values ###
opti.set_initial(k, .02)
opti.set_initial(kd, 0)
opti.set_initial(T, .2)
|
Solve:
Set up and solve the problem with the solver of your choice. I used IPOPT because that's what we used for Cheetah stuff. I played around with a few others and didn't get any better results.
1
2
3 | ### solve ###
opti.solver("ipopt") # set numerical backend
sol = opti.solve() # actual solve
|
And that's it.
Here an example solution:
Here you can see how the kinetic energy of the mass, of the rotor inertia, and the potential energy of the mass trade off over the trajectory:
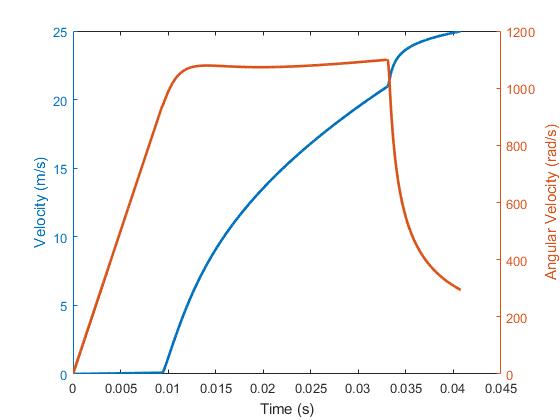
Compared to the hand-designed version of the transmission profile, the optimized one can exactly max out my acceleration constraint, exactly max out the motor speed constraint, and rapidly decelerate the motor to my threshold at the end (ignore the acceleration at the last timestep, it's not meaningful):
Below is an example of an optimized transmission ratio vs rotor angle on the left, vs my hand-designed one on the right. The mass/torque/inertia/stroke used for these are different, so the absolute numbers shouldn't be compared, but qualitatively, I was definitely on the right track with my hand-design. Which is always satisfying to see:
The numbers I'm seeing out of the optimization are nearly 10 meters (if I can hit the weight target in there), so things are going to get exciting.